4.1 Introdução

Este capítulo não é uma peculiaridade da Mecânica dos Fluidos, porém para ela ocupa um papel relevante, já que parte de seu desenvolvimento teve origem experimental.

Vamos inicialmente mostrar a vantagem de recorrermos a análise dimensional no estudo de certas aplicações da engenharia.

Consideremos a seguinte aplicação:

• Estuda-se em laboratório a força de resistência (força de arraste) que um dado fluido (ρ₁ e µ₁) exerce no deslocamento de uma esfera (de diâmetro D) em seu meio. A experiência realizada para o referido estudo é representada pela figura 4.1

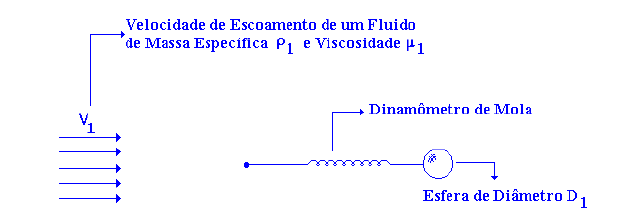
Figura 4.1

Variando-se a velocidade v₁ , para uma dada esfera de diâmetro D₁ e para um dado fluido (ρ₁ e µ₁), pode se obter a tabela apresentada a seguir:

v1 (m/s)	....	....	....	....
F1 (N)	....	....	....	....

Através da tabela anterior, obtém-se a curva representada pela figura 4.2.

Figura 4.2

Podemos constatar facilmente que a curva representada na figura 4.2 é uma curva particular, mesmo porque apresenta, tanto na ordenada como na abscissa, grandezas dimensionais.

objetivo

Generalizar as informações obtidas em laboratório.

Para que possamos exemplificar o objetivo mencionado anteriormente, vamos supor que nos seja dirigida a seguinte questão:

“Qual a força exercida em uma esfera de diâmetro D₂ ; quando esta se desloca no mesmo fluido com a velocidade v₂?”

Condição: A resposta da questão deve ser obtida sem se recorrer a ensaios.

É justamente para satisfazer esta condição que recorremos à análise dimensional.

Temos as seguintes variáveis que causam influência no fenômeno: F - força de arraste, D - diâmetro da esfera, v - velocidade da esfera ou velocidade do fluido, ρ - massa específica do fluido e µ - viscosidade do fluido.

A análise dimensional determina os números adimensionais (números puros) que definem o fenômeno estudado. Para o exemplo anterior, temos:

Pelo fato das duas situações: a ensaiada em laboratório e a é questionada, serem semelhantes, podemos afirmar que ambas são caracterizadas pelas mesmas variáveis, o que equivale a dizer que π₁ e π₂ definem as duas situações.

Podemos a partir dos dados obtidos no ensaio, obter a tabela representada a seguir:

A partir da tabela anterior, podemos obter a curva universal do fenômeno, figura 4.3, que é aquela que tanto na ordenada como na abscissa, temos números adimensionais (números universais); o que equivale a dizer que, valem tanto para o fenômeno ensaiado em laboratório como para o fenômeno que é questionado.

Pela condição de semelhança, podemos escrever que:

Figura 4.3

Para o fenômeno questionado, temos os seguintes dados: ρ₂ = ρ₁; µ₂ = µ₁ ; D₂ e v₂, e isto nos permite calcular:

que pela condição de semelhança é igual a p_2)ensaiado.

Marcando π_2)q = π_2)e na abscissa da curva universal, podemos ler, na ordenada p_1)ensaiado, que pela condição de semelhança e igual a p_{1)questionado}.

, e isto permite calcular a força F₂ sem recorrer a ensaios, já que: F₂ =“A”× ρ₂ ×v₂×D₂

 

4.2 Função Característica

Representa as variáveis que causam influência no fenômeno.

Exemplo : f (F, V, ρ, µ, D) = 0

 

4.3 Grandezas Fundamentais

As grandezas fundamentais adotadas para os fenômenos da Mecânica dos Fluidos, geralmente são: F - Força; L - Comprimento e T - Tempo

 

4.4 Grandezas Derivadas

As grandezas derivadas de um fenômeno são todas as demais grandezas, excluindo-se as grandezas fundamentais.

 

4.5 Equação Dimensional

É a forma usada para definirmos uma grandeza derivada em função das grandezas fundamentais.

As equações dimensionais geralmente são escritas em forma de produto de potências, onde as bases são constituídas pelas grandezas fundamentais e os expoentes indicam o grau de dependência da grandeza derivada em função das grandezas fundamentais.

Exemplos:

[F] = F ® G.F.

[V] = L x T^-1 ® G.D.

[ρ] = F x L^-4 x T² ® G.D.

[µ] = F x L^-2 x T ® G.D.

[D] = L ® G.F.

 

4.6 Números Adimensionais - π

São números puros, obtidos através de uma combinação adequada das variáveis que causam influência no fenômeno.

A equação dimensional de um número adimensional será sempre: [π] = F⁰ L⁰ T⁰, sendo esta a forma de verificarmos se o mesmo é ou não número adimensional.

Exemplo:

Voltar